关于最短路径的几个算法

Code

Flody-Warshall算法




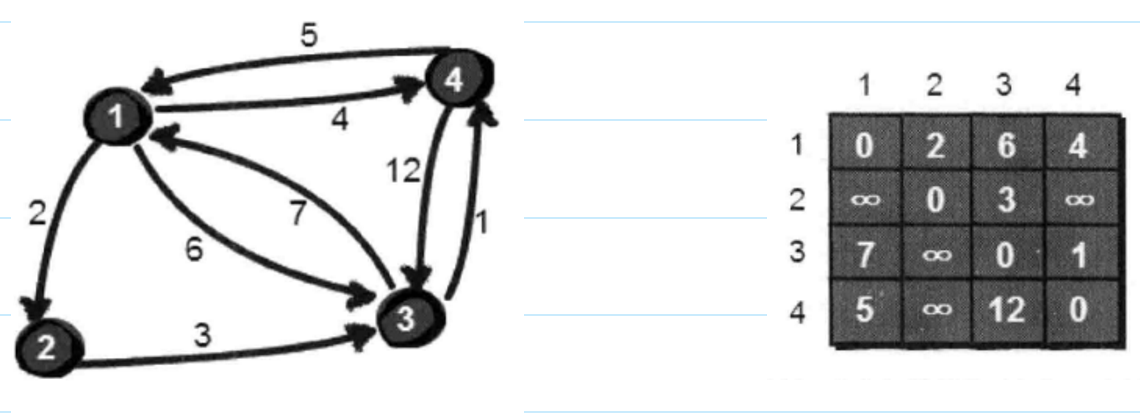
求任意两点之间的最短路径。称为“多源最短路径”
## 分析
如果要让任意两点（a到b）之间的路径变短，只能引入第三个点（k），有时候甚至不止一个k
若只允许经过1号顶点。只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示从i号顶点到j号顶点之间的路程。
只允许经过1号顶点
1
2
3
4
for(i=1;i<=n;i++)
    for(j=1;j<=n;j++)
        if(e[i][j]>e[i][1]+e[1][j])
            e[i][j]=e[i][1]+e[1][j];





只允许经过1号和2号顶点
1
2
3
4
5
6
7
8
for(i=1;i<=n;i++)
    for(j=1;j<=n;j++)
        if(e[i][j]>e[i][1]+e[1][j])
            e[i][j]=e[i][1]+e[1][j];
for(i=1;i<=n;i++)
    for(j=1;j<=n;j++)
        if(e[i][j]>e[i][2]+e[2][j])
            e[i][j]=e[i][2]+e[2][j];





只允许经过1号2号3号顶点



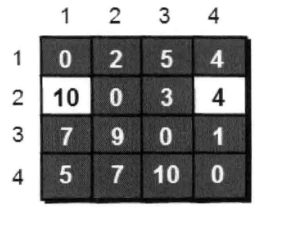
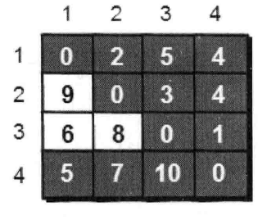
最终


实现代码

1
2
3
4
5
for(k=1;k<=n;k++)
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            if(e[i][j]>e[i][K]+e[K][j])
                e[i][j]=e[i][K]+e[K][j];

复杂度

时间复杂度：O(N^3)
空间复杂度：O(N^2)

特点

适用于稠密图和顶点关系密切的图
不能解决负权回路

Dijkstra算法



求1到23456最短路径。“单源最短路径”问题

分析

我们建立一个数组dis。用于存放1号顶点到其余各个顶点的距离。



先找出一个离1号顶点最近的顶点。
找出的是2号顶点。
讨论2-3这条路径能否让1到3的路径变短，也就是比较dis[3]和dis[2]+e[2][3]的大小。
可知dis[3]>dis[2]+e[2][3]。我们称为“松弛”
同理2-4，将dis[4]松弛为4
都松弛完毕之后，将2号顶点在book数组中标记起来



接下来在剩下的3456顶点中，选出离1号顶点最短的顶点。
当前离1号顶点最近的是4号顶点。因此dis[4]从“估计值”变为“确定值”
接下来对4号顶点的所有相邻点进行松弛（4-5，4-6，4-3）
都松弛完毕之后，将4号顶点在book数组中标记起来



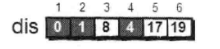
接下来在剩下的356顶点中，选出离1号顶点最短的顶点。
当前离1号顶点最近的是3号顶点。因此dis[3]从“估计值”变为“确定值”
接下来对3号顶点的所有相邻点进行松弛（3-5）
都松弛完毕之后，将3号顶点在book数组中标记起来



接下来在剩下的56顶点中，选出离1号顶点最短的顶点。
当前离1号顶点最近的是5号顶点。因此dis[5]从“估计值”变为“确定值”
接下来对5号顶点的所有相邻点进行松弛（5-6）
都松弛完毕之后，将5号顶点在book数组中标记起来



最后对6号顶点进行松弛



Dijkstra算法的主要思想：通过”边“来松弛1号顶点到其他顶点的距离。

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 初始化dis数组
for(i=1;i<=n;i++)
    dis[i]=e[1][i];
// 初始化book数组
for(i=1;i<=n;i++)
    book[i]=0;
book[1]=1;
for(i=1;i<=n;i++)
{
    min=inf;//inf假设为无限
    // 找出离1号顶点最近的顶点
    for(j=1;j<=n;j++)
    {
        if(book[j]==0&&dis[j]<min)
        {
            min=dis[j];
            u=j;
        }
    }
    book[u]=1;
    for(v=1;v<=n;v++)
    {
        if(e[u][v]<inf)
        {
            if(dis[v]>dis[u]+e[u][v])
                dis[v]=dis[u]+e[u][v];
        }
    }
}

复杂度

时间复杂度：O(N^2)
空间复杂度：O(M)

优化

  1. 可用堆降低至O(logN)
  2. 可用邻接表降至O(M+N)logN

邻接表

对于边数M少于N^2的系数图，可以使用相邻接表代替邻接矩阵。使得事件复杂度降至O(M+N)logN
对于M=N^2，O(M+N)logN是要大于O(N^2)的

存入



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// n为顶点数，m为边数
int n,m,i;
// u为开始点，v为结束点，w为权值
int u[6],v[6],w[6];
int first[5],next[5];
// 初始化first
for (i = 1; i <= n; i++)
{
    first[i]=-1
}
// 输入
// 1 4 9
// 2 4 6
// 1 2 5
// 4 3 8
// 1 3 7
for(i=1;i<=m;i++)
{
    scanf("%d %d %d",&u[i],&v[i],&w[i]);
    next[i]=first[u[i]];
    first[u[i]]=i;
}


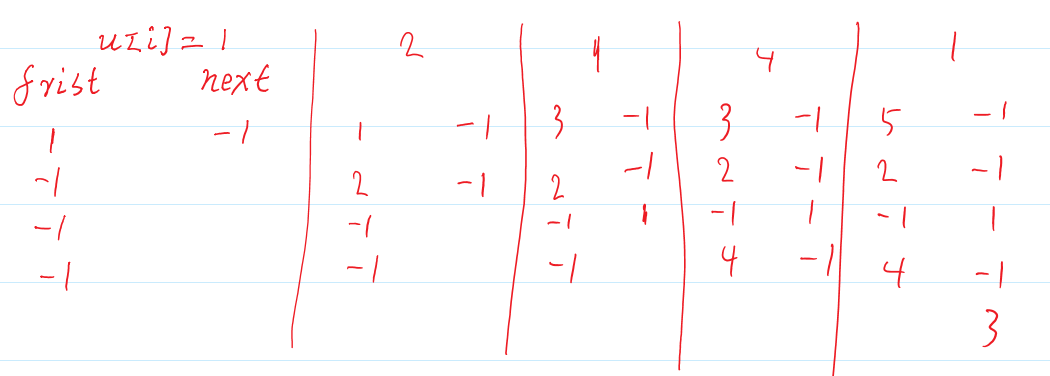
first是存放顶点对应的边数的数组，如果一个顶点有多条边，可以使用next遍历。
如：

1
2
3
4
5
// 1 4 9
// 2 4 6
// 1 2 5
// 4 3 8
// 1 3 7

顶点1对应有3条边；2，4有1条，3无。
遍历



1
2
3
4
5
6
7
8
9
for (int i = 0; i < n; ++i)
{
    k=first[i];
    while(k!=-1)
    {
        // do somethings
        k=next[k];
    }
}

Bellman-Ford算法

解决负权边问题



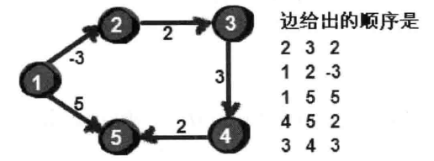
核心代码

v,u,w数组分别一一对应给出的边
n为顶点数，m为边数

1
2
3
4
for (int k = 1; k <= n-1; ++k) 
    for (int i = 1; i <= m; ++i)   //枚举每一条边
        if(dis[v[i]]>dis[u[i]]+w[i])   //对每一条边进行松弛
            dis[v[i]]=dis[u[i]]+w[i]

分析



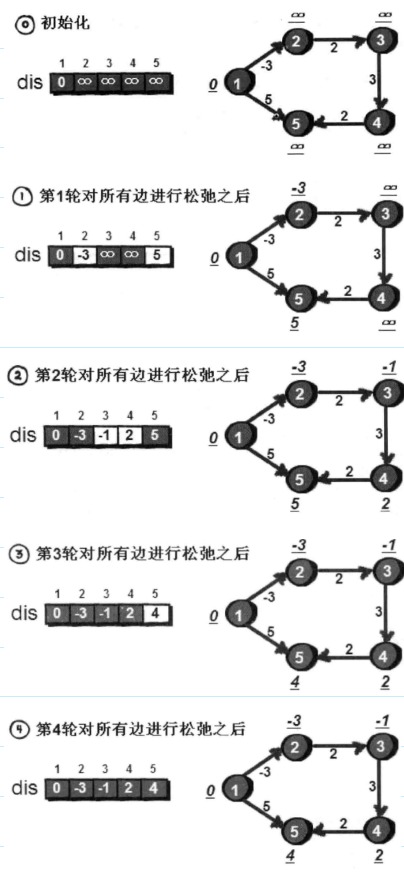
第一轮在对所有的边进行松弛之后，得到的是从1号顶点“只能经过一条边”到达其余各顶点的最短路径长度。
第二轮在对所有的边进行松弛之后，得到的是从1号顶点“最多经过两条边”到达其余各顶点的最短路径长度。
只需进行n-1轮。因为在一个含有n个顶点的图中，任意两点之间的最短路径最多包含n-1边
最短路径肯定是一个不包含回路的简单路径。
回路分为正权回路与负权回路
正权回路：回路权值为正。去掉这个回路会得到更短的路径。
负权回路：回路权值为负。每走一次会得到更短的路径。
Bellman-Ford算法还可以检测一个图是否存在负权回路
如果在进行n-1轮松弛之后，依然存在：

1
2
if(dis[v[i]]>dis[u[i]]+w[i])
    dis[v[i]]=dis[u[i]]+w[i]

复杂度

时间复杂度：O(NM)，比Dijkstra还要高
空间复杂度：O(M)

优化

  1. Bellman-Ford算法经常会在未到达n-1轮松弛前就已经计算出最短路径。如果在新一轮的松弛中数组dis没有发生变化。就可以跳出循环。
  2. Bellman-Ford的队列优化每次选取队首顶点u，对顶点u的所有出边进行松弛操作。如，有一条u-v，如果通过u-v这条边使得源点到顶点v的最短路径变短。(dis[u]+e[u][v]<dis[v])，且顶点v不在当前的队列中，就将顶点v放入队尾。我们还需要对队列中的顶点去重对顶点u的所有出边松弛完毕之后，将顶点v出队。
    接下来不断从队列中取出新的队首顶点再进行如上操作直至队列为空。
    实例分析




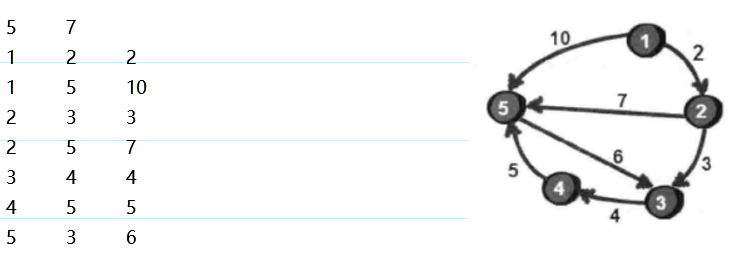
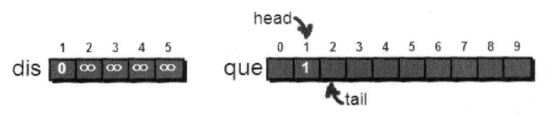
取1-2，dis[1]+e[1][2]<dis[2]。入队

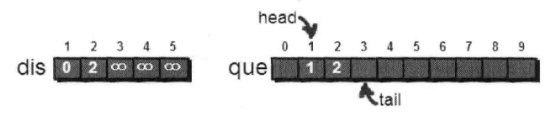
取1-5



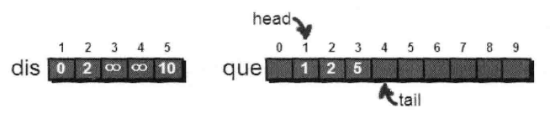
1号顶点处理完毕。出队
取2-3,2-5。处理2-5的时候，由于5号顶点已经在队列中，所以不能再次入队。




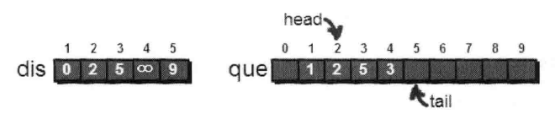
如此类推。最终处理结果




实现代码
本例使用邻接表存储
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// n为顶点数，m为边数
int n,m,i;
// u为开始点，v为结束点，w为权值
int u[6],v[6],w[6];
int first[5],next[5];
// book数组用于记录那些顶点已经在队列中
int dis[6],book[6]={0};
int que[101]={0},head=1,tail=1;
for (i = 1; i <=n; i++)
{
    dis[i]=inf;
}
dis[1]=0;
for (i = 1; i <= n; i++) book[i]=0;
// 初始化first
for (i = 1; i <= n; i++)
{
    first[i]=-1
}
// 输入
// 1 4 9
// 2 4 6
// 1 2 5
// 4 3 8
// 1 3 7
for(i=1;i<=m;i++)
{
    scanf("%d %d %d",&u[i],&v[i],&w[i]);
    next[i]=first[u[i]];
    first[u[i]]=i;
}
que[tail]=1;tail++;        //入队
book[1]=1;                //标记
while(head<tail)
{
    k=first[que[head]];
    while(k!=-1)        //扫描当前顶点所有的边
    {
        if(dis[v[k]]>dis[u[k]]+w[k])
        {
            dis[v[k]]=dis[u[k]]+w[k];
            // 去重
            if(book[v[k]]==0)
            {
                que[tail]=v[k];
                tail++;
                book[v[k]]=1;
            }
        }
        k=next[k];
    }
    // 出队
    book[que[head]]=0;
     head++;
}

队列优化的Bellman-Ford算法：其实上就是只处理那些在前一遍松弛中改变了最短路径估计值的顶点（因为只有这样才可能引起它们的邻接点最短路径估计值发生改变。）
使用队列优化的Bellman-Ford算法在形式上和广度优先搜索非常类似，不同的是在广度优先搜索的时候一个顶点出队后通常就不会再重新进入队列。
当一个顶点的最短路径估值变小后，需要重新进行松弛。
如果某个点进入队列的次数超过n次，则这个图有负环。
复杂度
最坏的情况下为O(NM)

本文标题:关于最短路径的几个算法

文章作者:Vincent Zhong

发布时间:2016-08-16, 12:25:36

最后更新:2019-07-07, 13:13:09

原始链接:https://wax8280.github.io/2016/08/16/关于最短路径的几个算法/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. Flody-Warshall算法
    1. 1.1. 实现代码
    2. 1.2. 复杂度
    3. 1.3. 特点
  2. 2. Dijkstra算法
    1. 2.1. 分析
    2. 2.2. 实现代码
    3. 2.3. 复杂度
      1. 2.3.1. 优化
        1. 2.3.1.1. 邻接表
  3. 3. Bellman-Ford算法
    1. 3.1. 核心代码
    2. 3.2. 分析
    3. 3.3. 复杂度
      1. 3.3.1. 优化
|