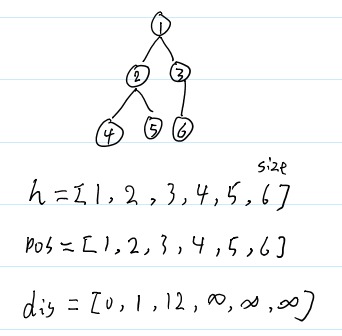关于Dijkstra算法的具体步骤可以参考关于最短路径的几个算法
Dijkstra算法里面每次找出离源点最近之点,使用了两个嵌套的循环语句。导致时间复杂度为O(N^2)。
本例通过最小堆,优化这两个嵌套的循环语句。令算法整体复杂度降为O(NlogN)。
实现代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123
| #include<stdio.h> int dis[8]; int h[7], pos[7], size; int n=6, m=9,k; int inf = 99999999; int i, j; int u[10], v[10], w[10]; int first[7], next[10]; void swap(int x, int y) { int t; t = h[x]; h[x] = h[y]; h[y] = t; t = pos[h[x]]; pos[h[x]] = pos[h[y]]; pos[h[y]] = t; } void siftdown(int i) { int t, flag = 0; while (i * 2 <= size&&flag == 0) { if (dis[h[i]] > dis[h[i * 2]]) t = i * 2; else t = i; if (i * 2 + 1 <= size) { if (dis[h[t]]>dis[h[i * 2 + 1]]) t = i * 2 + 1; } if (t != i) { swap(t, i); i = t; } else flag = 1; } } void siftup(int i) { int flag = 0; if (i == 1) return; while (i != 1 && flag == 0) { if (dis[h[i]]<dis[h[i / 2]]) swap(i, i / 2); else flag = 1; i = i / 2; } } int pop() { int t; t = h[1]; h[1] = h[size]; pos[h[1]] = 1; size--; siftdown(1); return t; } int main() { int count = 0; for (i = 1; i <= m; i++) scanf("%d %d %d", &u[i], &v[i], &w[i]); dis[1] = 0; for (i = 2; i <= n; i++) dis[i] = inf; for (i = 1; i <= n; i++) first[i] = -1; for (i = 1; i <= m; i++) { next[i] = first[u[i]]; first[u[i]] = i; } count++; k = first[1]; while (k != -1) { dis[v[k]] = w[k]; k = next[k]; } size = n; for (i = 1; i <= size; i++){ h[i] = i; pos[i] = i; } for (i = size / 2; i >= 1; i--){ siftdown(i); } pop(); while (count < n) { j = pop(); count++; k = first[j]; while (k != -1) { if (dis[v[k]]>dis[u[k]] + w[k]) { dis[v[k]] = dis[u[k]] + w[k]; siftup(pos[v[k]]); } k = next[k]; } } for (i = 1; i <= n; i++) printf("%d ", dis[i]); return 0; }
|
输入
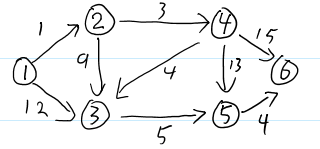
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
结果
0 1 8 4 13 17
分析
h是堆,值为顶点号;pos的值对应顶点在堆中的位置。
h与pos配合,形成最小堆。注意,是根据各个顶点在dis中对应的离源点的距离生成最小堆。
第0次循环
第一次循环
将1号顶点出堆,size前移,根据1的出边(1-N,这里指的是1-2,1-3)更新dis。1号顶点变为确定值。并更新堆。
第二次循环
将2号顶点出堆,size前移,根据2的出边更新dis。2号顶点变为确定值。并更新堆
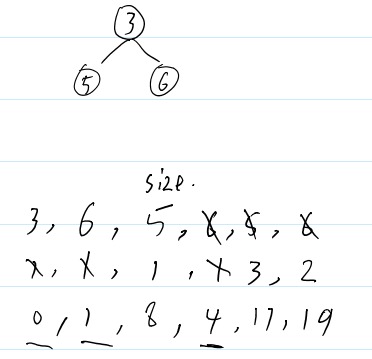
第三次循环
将四号顶点出堆,size前移,根据4的出边更新dis。4号顶点变为确定值。并更新堆
第四次循环
将三号顶点出堆,size前移,根据3的出边更新dis。3号顶点变为确定值。并更新堆
如此类推