用Canny进行边缘检测

Canny 边缘检测是一种非常流行的边缘检测算法，是 John F.Canny 在1986 年提出的。

1
2
3
4
5
6
7

import cv2
import numpy as np
img = cv2.imread("../lena.bmp", 0)
cv2.imwrite("canny.jpg", cv2.Canny(img, 200, 300))
cv2.imshow("canny", cv2.imread("canny.jpg"))
cv2.waitKey()
cv2.destroyAllWindows()

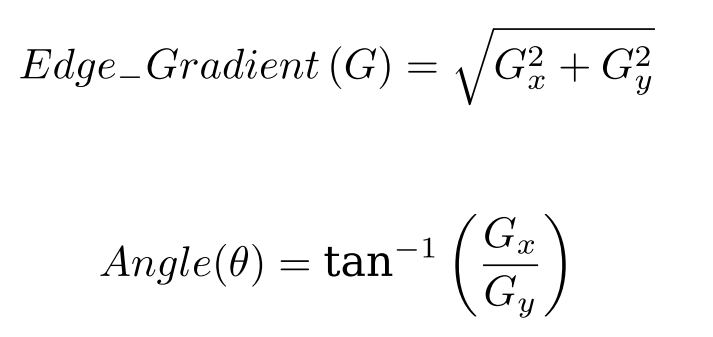
梯度的方向一般总是与边界垂直。梯度方向被归为四类：垂直，水平，和两个对角线。

• 非极大值抑制（Non-maximum suppression）
  在获得梯度的方向和大小之后，应该对整幅图像做一个扫描，去除那些非边界上的点。对每一个像素进行检查，看这个点的梯度是不是周围具有相同梯 度方向的点中最大的。如下图所示：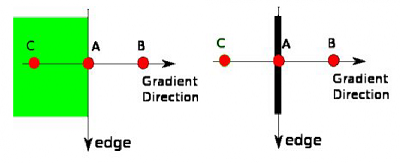
  
  
  
  
  
  现在你得到的是一个包含“窄边界”的二值图像。
• 双阀值的边缘检测防止误判（ a double threshold on all the detected edges to eliminate false positives）
  现在要确定那些边界才是真正的边界。这时我们需要设置两个阈值：
  minVal 和 maxVal。当图像的灰度梯度高于 maxVal 时被认为是真的边界， 那些低于 minVal 的边界会被抛弃。如果介于两者之间的话，就要看这个点是 否与某个被确定为真正的边界点相连，如果是就认为它也是边界点，如果不是 就抛弃。如下图：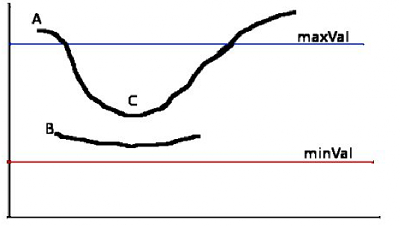
  
  
  
• 分析所有边和和他们相连的边，去掉虚边，保留实边

  轮廓检测

轮廓可以简单认为成将连续的点（连着边界）连在一起的曲线，具有相同的颜色或者灰度。轮廓在形状分析和物体的检测和识别中很有用。

• 为了更加准确，要使用二值化图像。在寻找轮廓之前，要进行阈值化处理或者 Canny 边界检测。
• 查找轮廓的函数会修改原始图像。如果你在找到轮廓之后还想使用原始图像的话，你应该将原始图像存储到其他变量中。
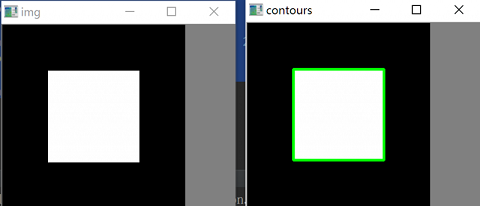
• 在 OpenCV 中，查找轮廓就像在黑色背景中超白色物体。你应该记住，要找的物体应该是白色而背景应该是黑色。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  # coding:utf-8 import cv2 import numpy as np img = np.zeros((200, 200), dtype=np.uint8) # 一个白色正方形 img[50:150, 50:150] = 255 # 阀值过滤 ret, thresh = cv2.threshold(img, 127, 255, 0) cv2.imshow("img", img) image, contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE) # 转换色彩空间 color = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR) img = cv2.drawContours(color, contours, -1, (0, 255, 0), 2) cv2.imshow("contours", color) cv2.waitKey() cv2.destroyAllWindows()

cv2.threshold：

作用：阀值处理；
参数：
输入
1.图像；
2.用来对像素值进行分类的阈值；
3.当像素值高于（有时是小于）阈值时应该被赋予的新的像素值；
4.阀值方法

• cv2.THRESH_BINARY
• cv2.THRESH_BINARY_INV
• cv2.THRESH_TRUNC
• cv2.THRESH_TOZERO
• cv2.THRESH_TOZERO_INV
  
  
  
  
  
  输出：
  retVal
  结果图像

cv2.findContours

作用：寻找轮廓
参数：
输入：
输入图像（会修改图像，可以使用img.copy()拷贝）
层次结构类型（hierarchy type）
轮廓近似方法（contour approximation method）
输出：
修改后的图像
轮廓（contours）
轮廓的层次结构
轮廓（第二个返回值）是一个 Python 列表，其中存储这图像中的所有轮廓。每一个轮廓都是一个 Numpy 数组，包含对象边界点（x，y）的坐标。
层次结构类型hierarchy type

• cv2.RETR_TREE 检索整个层次结构图像的轮廓,使您能够建立轮廓之间的“关系”。在你想完全消除两个相同轮廓的时候很有用。（在绝大多数情况下,你不需要检测一个物体在另一个具有相同类型的对象的里面）
• CV_RETR_EXTERNAL 只检测出最外轮廓即c0。
• CV_RETR_LIST 检测出所有的轮廓并将他们保存到表(list)中
• CV_RETR_COMP 检测出所有的轮廓并将他们组织成双层的结构
• CV_RETR_TREE 检测出所有轮廓并且重新建立网状的轮廓结构
  
  
  
  

  轮廓近似方法（contour approximation method）

• CHAIN_CODE 用freeman链码输出轮廓，其他方法输出多边形(顶点的序列)。
• CHAIN_APPROX_NONE将链码编码中的所有点转换为点。也就是参数contours中的每个轮廓是用构成该轮廓的所有像素点表示的。
• CHAIN_APPROX_SIMPLE压缩水平，垂直或斜的部分，只保存最后一个点。也就是说参数contours中的每个轮廓是用该轮廓的所有顶点表示的。
• CHAIN_APPROX_TC89_L1，CV_CHAIN_QPPROX_TC89_KCOS使用Teh-Chin链逼近算法中的一个。
• LINK_RUNS与上述的算法完全不同，连接所有的水平层次的轮廓。
  
  
  
  

  cv2.drawContours

• image,//要绘制轮廓的图像
• contours,//所有输入的轮廓，每个轮廓被保存成一个point向量
• ontourIdx,//指定要绘制轮廓的编号，如果是负数，则绘制所有的轮廓
• color,//绘制轮廓所用的颜色
• thickness=None //绘制轮廓的线的粗细，如果是负数，则轮廓内部被填充
• lineType=None, /绘制轮廓的线的连通性
• hierarchy=None,//关于层级的可选参数，只有绘制部分轮廓时才会用到
• maxLevel=None//绘制轮廓的最高级别，这个参数只有hierarchy有效的时候才有效
• //maxLevel=0，绘制与输入轮廓属于同一等级的所有轮廓即输入轮廓和与其相邻的轮廓
• //maxLevel=1, 绘制与输入轮廓同一等级的所有轮廓与其子节点。
• //maxLevel=2，绘制与输入轮廓同一等级的所有轮廓与其子节点以及子节点的子节点
• offset=None

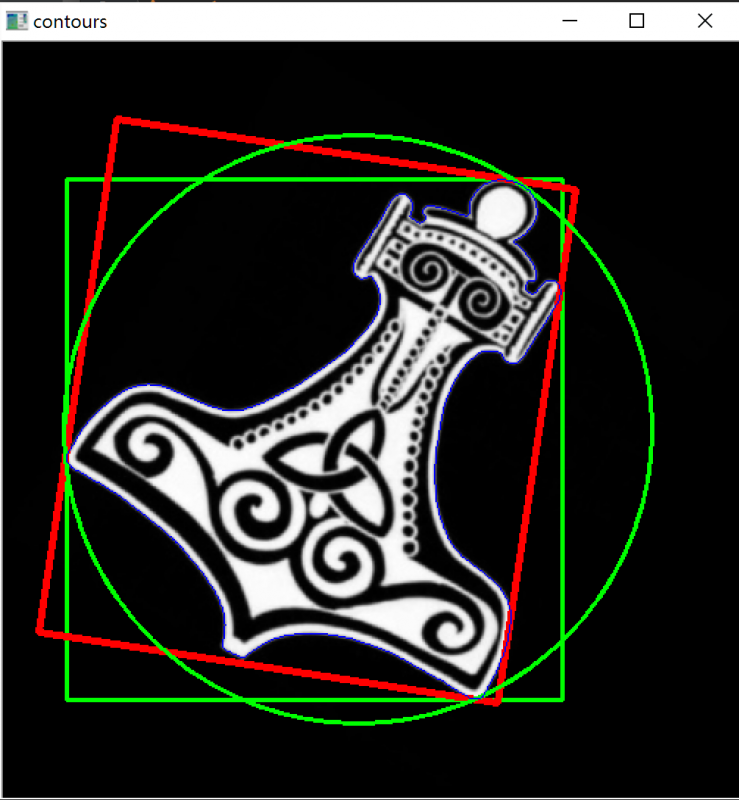
轮廓 –边界框,最小矩形区域和最小封闭圆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 我们先把图像转换成灰度图，然后使用cv2.threshold将图像二值化，处理完毕之后，绘制在原图上。
# coding:utf-8
import cv2
import numpy as np
# 读取图像，降低分辨率
img = cv2.pyrDown(cv2.imread("hammer.jpg", cv2.IMREAD_UNCHANGED))
# 转换成灰度图，进行简单阀值处理
# 这个本来不是80，而是127的，不过考虑到实际。还是将阀值降低，不然效果不好。
ret, thresh = cv2.threshold(cv2.cvtColor(img.copy(), cv2.COLOR_BGR2GRAY) ,
                            80, 255, cv2.THRESH_BINARY)
# 识别轮廓
image, contours, hier = cv2.findContours(thresh, cv2.RETR_EXTERNAL,
                                          cv2.CHAIN_APPROX_SIMPLE)
for c in contours:
    # 边界框坐标
    # 坐标x,y；宽度高度w,h
    x,y,w,h = cv2.boundingRect(c)
    # 绘制矩形（绿色
    cv2.rectangle(img, (x,y), (x+w, y+h), (0, 255, 0), 2)
    # 找出最小区域（OpenCV没有直接求出最小区域坐标的函数，我们需要转换）
    rect = cv2.minAreaRect(c)
    # 计算最小矩形区域的坐标（结果为float）
    box = cv2.boxPoints(rect)
    # 正常化坐标。将其化成整数
    box = np.int0(box)
    # 绘制轮廓（红色；第三个参数，数组索引0开始
    cv2.drawContours(img, [box], 0, (0,0, 255), 3)
    # 计算最小封闭圆的中心与半径（绿
    (x,y),radius = cv2.minEnclosingCircle(c)
    # 转换成int
    center = (int(x),int(y))
    radius = int(radius)
    # 绘制圆形
    img = cv2.circle(img,center,radius,(0,255,0),2)
cv2.drawContours(img, contours, -1, (255, 0, 0), 1)
cv2.imshow("contours", img)
cv2.waitKey()
cv2.destroyAllWindows()

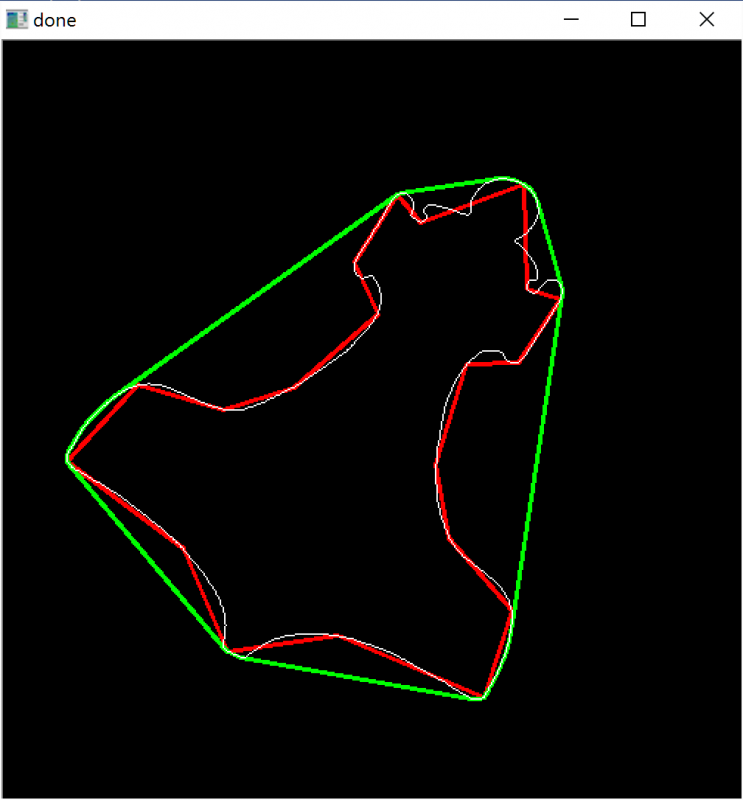
轮廓——凸轮廓线（convex contours）和道格拉斯·皮克雷算法（Douglas-Peucker algorithm）

将轮廓形状近似到另外一种由更少点组成的轮廓形状，新轮廓的点的数目 由我们设定的准确度来决定。使用的Douglas-Peucker算法。
OpenCV里面检测近似边界多边形（approximate bounding polygon of a shape）的函数
cv2.approxPolyDP
参数：
输入：
轮廓
一个ε值，代表原图跟近似多边形的最大差值（值越低，近似的值就约接近原来的轮廓）
一个布尔值，表示多边形是否是封闭的
为什么需要一个近似边界多边形，特别是当我们有一个精确的轮廓的时候。
答案是，多边是是一组直线的集合，多边形在计算机视觉处理里面十分重要

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# coding:utf-8
import cv2
import numpy as np
# 读取图像，降低分辨率
img = cv2.pyrDown(cv2.imread("hammer.jpg", cv2.IMREAD_UNCHANGED))
# 转换成灰度图，进行简单阀值处理
# 这个本来不是80，而是127的，不过考虑到实际。还是将阀值降低，不然效果不好。
ret, thresh = cv2.threshold(cv2.cvtColor(img.copy(), cv2.COLOR_BGR2GRAY) ,
                            80, 255, cv2.THRESH_BINARY)
# 识别轮廓
image, contours, hier = cv2.findContours(thresh, cv2.RETR_EXTERNAL,
                                          cv2.CHAIN_APPROX_SIMPLE)
cnt = contours[0]
img = np.zeros((img.shape[0], img.shape[1],3), dtype=np.uint8)
# 求周长，True表示闭合
epsilon = 0.01 * cv2.arcLength(cnt, True)
# 近似多边形，True表示闭合
approx = cv2.approxPolyDP(cnt, epsilon, True)
# 直接使用轮廓，制作凸型（convex shapes）
hull = cv2.convexHull(cnt)
cv2.drawContours(img, [approx], 0, (0,0, 255), 2)
cv2.drawContours(img, [hull], 0, (0,255, 0), 2)
cv2.drawContours(img, contours, -1, (255, 255, 255), 1)
cv2.imshow("done", img)
cv2.waitKey()

线与圆形检测

线条和形状检测有其背后的理论基础在一种叫做Hough变换的技术，由Richard Duda 和 Peter Hart发明。

线段检测

HoughLines和HoughLinesP一个使用标准霍夫变换，另一个使用概率霍夫变换。通常，后者速度更快
原理
霍夫变换在检测各种形状的的技术中非常流行，如果你要检测的形状可以 用数学表达式写出，你就可以是使用霍夫变换检测它。及时要检测的形状存在
一点破坏或者扭曲也可以使用。我们下面就看看如何使用霍夫变换检测直线。 一条直线可以用数学表达式 y = mx + c 或者 ρ = xcos θ + y sin θ 表示。
ρ 是从原点到直线的垂直距离，θ 是直线的垂线与横轴顺时针方向的夹角（如 果你使用的坐标系不同方向也可能不同，我是按 OpenCV 使用的坐标系描述 的）。如下图所

所以如果一条线在原点下方经过，ρ 的值就应该大于 0，角度小于 180。 但是如果从原点上方经过的话，角度不是大于 180，也是小于 180，但 ρ 的值 小于 0。垂直的线角度为 0 度，水平线的角度为 90 度。 让我们来看看霍夫变换是如何工作的。每一条直线都可以用 (ρ, θ) 表示。 所以首先创建一个 2D 数组（累加器），初始化累加器，所有的值都为 0。行表 示 ρ，列表示 θ。这个数组的大小决定了最后结果的准确性。如果你希望角度精 确到 1 度，你就需要 180 列。对于 ρ，最大值为图片对角线的距离。所以如果 精确度要达到一个像素的级别，行数就应该与图像对角线的距离相等。 想象一下我们有一个大小为 100x100 的直线位于图像的中央。取直线上

的第一个点，我们知道此处的（x，y）值。把 x 和 y 带入上边的方程组，然后 遍历 θ 的取值：0，1，2，3，. . .，180。分别求出与其对应的 ρ 的值，这样我 们就得到一系列（ρ, θ）的数值对，如果这个数值对在累加器中也存在相应的位 置，就在这个位置上加 1。所以现在累加器中的（50，90）=1。（一个点可能 存在与多条直线中，所以对于直线上的每一个点可能是累加器中的多个值同时 加 1）。

现在取直线上的第二个点。重复上边的过程。更新累加器中的值。现在累加器中（50,90）的值为 2。你每次做的就是更新累加器中的值。对直线上的 每个点都执行上边的操作，每次操作完成之后，累加器中的值就加 1，但其他地方有时会加 1, 有时不会。按照这种方式下去，到最后累加器中（50,90）的 值肯定是最大的。如果你搜索累加器中的最大值，并找到其位置（50,90），这 就说明图像中有一条直线，这条直线到原点的距离为 50，它的垂线与横轴的 夹角为 90 度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# coding:utf-8
import cv2
import numpy as np
img = cv2.imread('line.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray, 50, 150, apertureSize=3)
minLineLength = 3
maxLineGap = 200
# lines = cv2.HoughLinesP(edges, 1, np.pi / 180, 200)
# for line in lines:
# for x1, y1, x2, y2 in line:
# cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)
# 第一个参数是一个二值化图像（所以在进行霍夫变换之前要首先进行二值化，或者进行 Canny 边缘检测。）
# 第二三个参数分别代表 ρ 和 θ 的精确度
# 第四个参数是阈值，只有累加其中的值高于阈值时才被认为是一条直
lines = cv2.HoughLines(edges, 1, np.pi / 180, 200)
for line in lines:
    for rho, theta in line:
        a = np.cos(theta)
        b = np.sin(theta)
        x0 = a * rho
        y0 = b * rho
        x1 = int(x0 + 1000 * (-b))
        y1 = int(y0 + 1000 * (a))
        x2 = int(x0 - 1000 * (-b))
        y2 = int(y0 - 1000 * (a))
        cv2.line(img, (x1, y1), (x2, y2), (0, 0, 255), 2)
cv2.imshow("edges", edges)
cv2.imshow("lines", img)
cv2.waitKey()
cv2.destroyAllWindows()

圆形检测

使用霍夫变换在图像中找圆形（环）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# coding:utf-8
import cv2
import numpy as np
planets = cv2.imread('planet_glow.jpg')
gray_img = cv2.cvtColor(planets, cv2.COLOR_BGR2GRAY)
# 模糊
img = cv2.medianBlur(gray_img, 5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)
'''
cv2.HoughCircles(image, method, dp, minDist, circles, param1, param2, minRadius, maxRadius)
method:用于检测的方法，现在只有HOUGH_GRADIENT
dp:累加器分辨率：dp=1跟原图有同样的分辨率，dp=2分辨率是原图的一般
minDist：圆心到圆的最短距离
param1:First method-specific parameter。在HOUGH_GRADIENT里面，是Canny边缘检测较大的那个参数
param2:累加器在检测时候圆心的阀值。约小约容易检测到假圆
'''
cv2.imshow("Blur", img)
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,60, param1=130,
                              param2=30,minRadius=0,maxRadius=0)
circles = np.uint16(np.around(circles))
for i in circles[0,:]:
    # 圆
    cv2.circle(planets,(i[0],i[1]),i[2],(0,255,0),2)
    # 中心点
    cv2.circle(planets,(i[0],i[1]),2,(0,0,255),3)
cv2.imwrite("planets_circles.jpg", planets)
cv2.imshow("HoughCirlces", planets)
cv2.waitKey